Философия древней индии и древнего китая кратко. Философия Древнего Китая: кратко и информативно. Философия Древней Индии и Китая. Продовольствия российской федерации

статистическая оценка распределение выборка

Оценка - это приближение значений искомой величины, полученное на основании результатов выборочного наблюдения. Оценки являются случайными величинами. Они обеспечивают возможность формирования обоснованного суждения о неизвестных параметрах генеральной совокупности. Примером оценки генеральной средней является выборочная средняя генеральной дисперсии - выборочная дисперсия и т.д.

Для того чтобы оценить насколько «хорошо» оценка отвечает соответствующей генеральной характеристике разработаны 4 критерия: состоятельность, несмещенность, эффективность и достаточность. Этот подход основывается на том, что качество оценки определяется не по ее отдельным значениям, а по характеристикам ее распределения как случайной величины.

Основываясь на положениях теории вероятностей, можно доказать, что из таких выборочных характеристик, как средняя арифметическая, мода и медиана, только средняя арифметическая представляет собой состоятельную, несмещенную, эффективную и достаточную оценку генеральной средней. Этим и обуславливается предпочтение, отдаваемое средней арифметической в ряду остальных выборочных характеристик.

Несмещенность оценки проявляется в том, что ее математическое ожидание при любом объеме выборки равно значению оцениваемого параметра в генеральной совокупности. Если это требование не выполняется, то оценка является смещенной .

Условие несмещенности оценки направлено на устранение систематических ошибок оценивания.

При решении задач оценивания применяют также асимптотически несмещенные оценки , для которых при увеличении объема выборки математическое ожидание стремится к оцениваемому параметру генеральной совокупности.

Состоятельность статистических оценок проявляется в том, что с увеличением объема выборки оценка все больше и больше приближается к истинному значению оцениваемого параметра или, как говорят, оценка сходится по вероятности к искомому параметру, или стремится к своему математическому ожиданию. Лишь состоятельные оценки имеют практическую значимость.

Это такая оценка несмещенного параметра, которая обладает наименьшей дисперсией при данном объеме выборки. На практике дисперсия оценки обычно отождествляется с ошибкой оценки.

В качестве меры эффективности оценки принимают отношение минимально возможной дисперсии к дисперсии другой оценки.

Оценка, обеспечивающая полноту использования всей содержащейся в выборке информации о неизвестной характеристике генеральной совокупности, называется достаточной (исчерпывающей).

Соблюдение рассмотренных выше свойств статистических оценок дает возможность считать выборочные характеристики для оценки параметров генеральной совокупности лучшими из возможных.

Важнейшая задача математической статистики состоит в том, чтобы по выборочным данным получить наиболее рациональные, «правдивые» статистические оценки искомых параметров генеральной совокупности. Различают два вида статистических выводов: статистическая оценка; проверка статистических гипотез.

Основная задача получения статистических оценок заключается в выборе и обосновании наилучших оценок, обеспечивающих возможность содержательной оценки неизвестных параметров генеральной совокупности.

Задача оценки неизвестных параметров может быть решена двумя способами:

• 1. неизвестный параметр характеризуется одним числом (точкой) - используется метод точечной оценки;
• 2. интервальная оценка, то есть определяется интервал, в котором с некоторой вероятностью может находиться искомый параметр.

Точечная оценка неизвестного параметра заключается в том, что конкретное числовое значение выборочной оценки принимается за наилучшее приближение к истинному параметру генеральной совокупности, то есть неизвестный параметр генеральной совокупности оценивается одним числом (точкой), определенным по выборке. При таком подходе всегда существует риск совершить ошибку, поэтому точечная оценка должна дополняться показателем возможной ошибки при определенном уровне вероятности.

В качестве средней ошибки оценки принимается ее среднее квадратическое отклонение.

Тогда точечная оценка генеральной средней может быть представлена в виде интервала

где - выборочная средняя арифметическая.

При точечной оценке применяют несколько методов получения оценок по выборочным данным:

• 1. метод моментов, при котором моменты генеральной совокупности заменяются моментами выборочной совокупности;
• 2. метод наименьших квадратов;
• 3. метод максимального правдоподобия.

Во многих задачах требуется найти не только числовую оценку параметра генеральной совокупности, но и оценить ее точность и надежность. Особенно это важно для выборок относительно малого объема. Обобщением точечной оценки статистического параметра является его интервальная оценка - нахождение числового интервала, содержащего с определенной вероятностью оцениваемый параметр.

В связи с тем, что при определении генеральных характеристик по выборочным данным всегда присутствует некоторая ошибка, практичнее определить интервал с центром в найденной точечной оценке, внутри которого с некоторой заданной вероятностью находится истинное искомое значение оцениваемого параметра генеральной характеристики. Такой интервал называют доверительным.

Доверительный интервал - это числовой интервал, который с заданной вероятностью г накрывает оцениваемый параметр генеральной совокупности. Такую вероятность называют доверительной. Доверительная вероятность г - это вероятность, которую можно признать достаточной в рамках решаемой задачи для суждения о достоверности характеристик, полученных на основе выборочных наблюдений. Величину

вероятности допустить ошибку называют уровнем значимости .

Для выборочной (точечной) оценки И * (тета) параметра И генеральной совокупности с точностью (предельной ошибкой ) Д и доверительной вероятностью г доверительный интервал определяется равенством:

Доверительная вероятность г дает возможность установить доверительные границы случайного колебания изучаемого параметра И для данной выборки.

В качестве доверительной вероятности принимают зачастую следующие значения и соответствующие им уровни значимости

Таблица 1. - Наиболее употребительные доверительные вероятности и уровни значимости

Например, 5-процентный уровень значимости означает следующее: в 5-ти случаях из 100 существует риск совершить ошибку при выявлении характеристик генеральной совокупности по выборочным данным. Или, другими словами, в 95 случаях из 100 генеральная характеристика, выявленная на основе выборки будет лежать в пределах доверительного интервала.

Вопросы статистической оценки связывают в единое целое такие проблемные аспекты математической статистики, как научная методология, случайные величины, статистические распределения и др. Для любой выборки присущи ошибки, обусловленные неполнотой охвата единиц, ошибками измерения и тому подобными причинами. Такие ошибки в реальной жизни придают каждой гипотезе (в частности, сформулированной на базе экономических выводов) случайный, стохастический характер. Независимо от количества переменных, предусмотренных теоретическими гипотезами, делается предположение, что влияние различных видов ошибок может быть достаточно точно описан с помощью только одной составляющей. Такой методологический подход позволяет ограничиться одномерным распределением вероятностей при одновременном оценивании нескольких параметров.

Статистическая оценка - это один из двух типов статистического суждения (второй тип - проверка гипотез). Она представляет собой особого рода метод суждения о числовых значения характеристик (параметров) распределения генеральной совокупности по данным выборки из этой совокупности. То есть, имея результаты выборочного наблюдения, мы пытаемся оценить (с наибольшей точностью) значения определенных параметров, от которых зависит распределение признака (сменной), которая нас интересует, в генеральной совокупности. Поскольку выборка включает только часть единиц генеральной совокупности (иногда очень малое их число), существует риск допустить ошибку. Несмотря на уменьшение такого риска с увеличением числа единиц наблюдения, он все же имеет место при выборочном наблюдении. Отсюда, принятым по результатам выборки решением предоставляют вероятностный характер. Но было бы неверным рассматривать статистические суждения только с позиций вероятностей. Такой подход не всегда оказывается достаточным для построения правильных теоретических предположений относительно параметров генеральной совокупности. Часто нужен еще ряд дополнительных суждений, которые бы обеспечили более глубокое обоснование. Например, нужно оценить с возможно большим приближением значения средней численности квалифицированных рабочих на предприятиях региона. При этом оценивается средняя арифметическая переменной х из генеральной совокупности, которая имеет нормальное распределение. Получив выборку по данному признаку в количестве п единиц, необходимо решить вопрос: какую величину по данным выборки необходимо принять как наиболее близкую к средней в генеральной совокупности? Таких величин, математическое ожидание которых равна искомому параметру (или близкое к нему), можно привести несколько: а) средняя арифметическая; б) мода; в) медиана; г) средняя, исчисленная по размаху вариации, и т.д.

С вероятностной точки зрения каждой из названных выше величин можно считать дают наилучшее приближение к искомому параметра генеральной совокупности (х), поскольку математическое ожидание каждой из этих функций (особенно для больших выборок) равна генеральной средней. Обусловлено такое предположение тем, что при многократном повторении выборки из той же генеральной совокупности будет получен "в среднем" верный результат.

Правильность "в среднем" объясняется равенством повторений положительных и отрицательных отклонений возникающих ошибок оценки генеральной средней, то есть средняя ошибка оценки будет равна нулю.

В практических условиях, как правило, организуют одну выборку, поэтому исследователя интересует вопрос о более точную оценку искомого параметра по результатам конкретной выборки. Для решения такой задачи, кроме выводов, которые вытекают непосредственно из отвлеченного вычисления вероятностей, нужны дополнительные правила мотивации наилучшего приближения оценки к искомому параметра генеральной совокупности.

Существует достаточное количество способов оценки констант по выборочным наблюдениям. Какие из них лучшие в решении конкретных задач исследования - занимается теория статистического оценивания. Она исследует условия, которым должна подчиняться та или иная оценка, ориентирует на оценки, более предпочтительны при данных обстоятельствах. Теория оценок указывает на превосходство одной оценки по сравнению с другой.

Как известно, информация, полученная на основе выборки, не носит категорического характера в заключении. Если, например, изучаемых 100 голов животных по их заболевания здоровыми оказались 99, то существует вероятность, что одно животное, которое осталось необследованной именно носит в себе вирус предполагаемого заболевания. Поскольку это маловероятно, делается вывод об отсутствии данного заболевания. В большинстве случаев такой вывод полностью оправдывается.

Руководствуясь подобными выводами в практической деятельности, экспериментатор (исследователь) опирается не на достоверность информации, а только на ее вероятность.

Другая сторона выборочного наблюдения, как уже отмечалось, решает задачи возможно более объективного определения степени надежности получаемых выборочных оценок. Решению этой задачи пытаются предоставить как можно более точный вероятностный выражение, то есть речь идет об определении степени точности оценки. Здесь исследователь определяет границы возможного расхождения между оценкой, полученной при выборке, и действительным значением ее величины в генеральной совокупности.

Точность оценки обусловлено способом ее расчета по данным выборки и способом отбора единиц в выборочную совокупность.

Способ получения оценок предполагает любую вычислительную процедуру (метод, правило, алгебраическую формулу). Это приоритет теории статистического оценивания. Способы отбора ведут к вопросам техники осуществления выборочного исследования.

Изложенное выше позволяет дать определение понятию "статистическая оценка".

Статистическая оценка - это приближенное значение искомого параметра генеральной совокупности, которое получено по результатам выборки и обеспечивает возможность принятия обоснованных решений о неизвестных параметры генеральной совокупности.

Предположим, что ^ "- статистическая оценка неизвестного параметра ^ теоретического распределения. По многократно осуществляемыми одинакового

Объем выборки из генеральной совокупности найдены оценки и 2 ^ ""п,

имеющих разные значения. Поэтому оценку ^ ", можно рассматривать как

случайную величину, а +17 две, 3 ~ "п - как ее возможные значения. Как случайная величина, она характеризуется определенной функцией плотности вероятностей. Поскольку эта функция обусловлена результатом выборочного наблюдения (эксперимента), то ее называют выборочным распределением. Такая функция описывает плотность вероятности для каждой из оценок, используя определенное число выборочных

наблюдений. Если предположить, что, статистическая оценка ^ ", - это алгебраическая функция от определенного набора данных и такой набор будет получен при осуществлении выборочного наблюдения, то в

общем виде оценка получит выражение: ® п = f (Xl.X2, ^ 3, ... Х т).

По окончании выборочного обследования данная функция уже не является оценкой общего вида, а принимает - конкретное значение, то есть становится количественной оценке (числом). Иначе говоря, из вышеприведенного выражения функции следует, что любой из показателей, характеризующих результаты выборочного наблюдения, можно считать оценкой. Выборочная средняя является оценкой генеральной средней. Рассчитана по выборке дисперсия или вычислено с нее значение среднего квадратического отклонения являются оценками соответствующих характеристик генеральной совокупности и т.д

Как уже отмечалось, расчет статистических оценок не гарантирует исключения ошибок. Суть заключается в том, что последние не должны быть систематическими. Наличие их должно носить случайный характер. Рассмотрим методологическую сторону этого положения.

Допустим, оценка ^ "дает неточное значение оценки ^ генеральной совокупности с недостатком. В этом случае каждое вычислено значение = 1,2,3, ..., п) будет меньше действительное значение величины $.

По этой причине математическое ожидание (среднее значение) случайной величины в будет меньше, чем в, то есть (М (^ п. И, наоборот, если дает оценку с избытком, то и математическое ожидание

случайной ^ "станет больше, чем $.

Отсюда следует, что использование статистической оценки, математическое ожидание которой не равно оцениваемому параметру, приводит к систематическим погрешностям, то есть до неслучайных ошибок, которые искривляют результаты измерений в одну сторону.

Возникает естественное требование: математическое ожидание оценки ^ "должно равняться оцениваемому параметру. Соблюдение этого требования не устраняет ошибок в целом, поскольку выборочные значения оценки могут быть больше или меньше действительного значения оценки генеральной совокупности. Но ошибки в один и другую сторону от значений ^ будут встречаться (согласно теории вероятностей) с одинаковой частотой. Следовательно, соблюдение этого требования, математическое ожидание выборочной оценки должно равняться оцениваемому параметру, исключает получение систематических (неслучайных) ошибок, то есть

М (в) = 6.

Выбор статистической оценки, которая дает наилучшее приближение оцениваемого параметра, представляет собой важную задачу в теории оценивания. Если известно, что распределение исследуемой случайной величины в генеральной совокупности соответствует закону нормального распределения, то по выборочным данным необходимо оценить математическое ожидание и среднее квадратическое отклонение. Объясняется это тем, что названные две характеристики полностью определяют основы, на которых построено нормальное распределение. Если исследуемая случайная величина распределена по закону Пуассона, оценивают параметр ^, поскольку он определяет это распределение.

Математическая статистика различает такие методы получения статистических оценок по выборочным данным: метод моментов, метод максимума правдоподобия.

При получении оценок методом моментов моменты генеральной совокупности заменяются моментами выборочной совокупности (вместо вероятностей при весе используют частоты).

Чтобы статистическая оценка давала "наилучшее приближение" к генеральной характеристики, она должна иметь ряд свойств. О них речь пойдет ниже.

Возможность выбора наилучшей оценки обусловлено знанием их основных свойств и умением классифицировать оценки по этим свойствам. В математической литературе "свойства оценок" иногда называют "требования к оценкам" или "критерии оценок" .В основных свойств статистических оценок относятся: Несмещенность, эффективность, способность, достаточность.

Если принять, что выборочная средняя (~) и выборочная дисперсия

(Ств) являются оценками соответствующих генеральных характеристик (^), то есть их математическим ожиданием, учитываем, что при большом количестве

единиц выборки названы характеристики (~) будут приближены к их математических ожиданий. Если же число единиц выборки небольшой, эти характеристики могут значительно отличаться от соответствующих математических ожиданий.

Если среднее значение выборочных характеристик, выбранных в качестве оценки, соответствует значению генеральной характеристики, оценка называется несмещенной. Доказательством того, что математическое ожидание выборочной средней равна генеральной средней (м (х) = х), свидетельствует о том, что величина ~ является несмещенной генеральной

средней. Иначе обстоит дело с избирательной дисперсией (o). ее

М (СТ 2) = - о-2. .

математическое ожидание п, не равна генеральной

дисперсии. Итак, а ч является смещенной оценкой а ". Чтобы устранить систематическую ошибку и получить несмещенную оценку, выборочную

дисперсию умножают на поправку п - 1 (это следует из образования

в 2 _ 2 п п - 1 "п -1

приведенного выше уравнения: п).

Таким образом, при немногочисленной выборке дисперсия равна:

2 Цх, - ~) 2 п Е (х и - ~) 2

сг в = х - = -.

п п - 1 п -1

Дробь (п - 1) называют поправкой Бесселя. Математик Бесселя первого установил, что выборочная дисперсия является смещенной оценкой генеральной дисперсии и применил указанную поправку для корректировки

оценок. Для малых выборок поправка (п - 1) значительно отличается от 1. С увеличением числа единиц наблюдения она быстро приближается к 1. При п <> 50 разница между оценками исчезает, то есть

° ~ "- .С всего вышесказанного вытекают следующие определения требований несмещенности.

Несмещенной называют статистическую оценку, математическое ожидание которой при любом объеме выборки равен значению

параметра генеральной совокупности, то есть м (^) = 9; м (х) = х.

Категорию "математическое ожидание" изучают в курсе теории вероятностей. Это числовая характеристика случайной величины. Математическое ожидание приближенно равно среднему значению случайной величины. Математическим ожидания дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности. Допустим, выполнено п исследований, в которых случайная величина х приняла ш 1 раз значение ш 2 раз значение Ш и раз значение Х к. При этом Ш 1 + Ш 2 + Ш 3 + ... + Ш к = п. Тогда сумма всех значений, принятых х, равна

х 1 ш 1 + х 2 ш 2 + х 3 ш 3 + ... + х к ш к

Средняя арифметическая этих значений составит:

Х 1 ш 1 + х 2 ш 2 + х 3 ш 3 + ... + х к ш к - ш 1 ^ ш 2 ^ ш 3 ^ ^ ш к

п или 1 п 2 п 3 п 1 п.

Поскольку п - относительная частота ^ значение х ^ п - относительная частота значения х 2 и т.д., приведенное выше уравнение примет вид:

Х = Х 1 № 1 + Х 2 № 2 + Х 3 № 3 + ... + Х к Н> к

При большом количестве выборочных наблюдений относительная частота примерно равна вероятности появления события, то есть

и> 1 = Л; ^ 2 = Щ = ™ к = Рк а потому х 2 х 1 р 1 + х 2 р 2 + Х 3 г. 3 + ... + Х КРК. Тогда

х ~ м (х) вероятностный смысл полученного результата расчетов заключается в том, что математическое ожидание приближенно равно (тем точнее, чем больше выборка) среднему арифметическому наблюдаемых значений случайной величины [М (х -) = ~ 1.

Критерий несмещенности гарантирует отсутствие систематических ошибок в оценке параметров генеральной совокупности.

Заметим, что выборочная оценка (^) - случайная величина, значение которой может меняться от одной выборки к другой. Мере ее вариации (рассеивания) вокруг математического ожидания параметра генеральной совокупности # характеризует дисперсия ст2 (^).

Пусть в-и В - - две несмещенные оценки параметра ^, то есть М (в ") = 6 и М (д,) = в. Дисперсии их в 1 (в -) и в г ф -). С двух 0 эти нок В Арто отдать предпочтение той, которая имеет меньшее рассеивание вокруг оцениваемого параметра. Если дисперсия оценки ^ "меньше дисперсии

оценки Сп, то за оценку & принимается первая, то есть ^ ".

Несмещенная оценка ^, что имеет наименьшую дисперсию среди всех возможных несмещенных оценок параметра ^, вычисленных по выборкам одинакового объема, называется эффективной оценкой. Это - второе свойство (требование) статистических оценок параметров генеральной совокупности. Надо, помнить, что эффективная оценка параметра генеральной совокупности, подчиненной определенному закону распределения, не совпадает с эффективной оценкой параметра второго раздела.

При рассмотрении выборок большого объема статистические оценки должны иметь свойство способности. Оценка способна (применяется также термин "пригодна" или "согласована") означает, что чем больше объем выборки, тем больше вероятность того, что ошибка оценки не превысит сколько угодно малого положительного

числа Е. Оценка 6 параметра ^ называется состоятельной, если она подчиняется закону больших чисел, то есть выполняется следующее равенство:

/ шг | г в-в <Е} = 1.

Как видим, способной называют такую статистическую оценку, которая при п приближается по вероятности к оцениваемому параметра. Другими словами, это значение показателя, полученное по выборке и приближающегося (совпадает по вероятности) вследствие закона больших чисел при увеличении объема выборки к своему математического ожидания. Например, если дисперсия несмещенной оценки при п стремится к нулю, то такая оценка оказывается и состоятельной, поскольку имеет наименьшее возможное дисперсию (при заданном объеме выборки).

Способными оценкам являются:

1) доля признака в выборочной совокупности, то есть частость как оценка доли признака в генеральной совокупности;

2) выборочная средняя как оценка генеральной средней;

3) выборочная дисперсия как оценка генеральной дисперсии;

4) выборочные коэффициенты асимметрии и эксцесса как оценка генеральных коэффициентов.

В литературе по математической статистике почему-то не всегда можно встретить описание четвертой свойства статистических оценок -достатнисть. Оценка достаточное (или исчерпывающая) - это оценка, которая приводит (обеспечивает) полноту охвата всей выборочной информации о неизвестном параметр генеральной совокупности. Таким образом, достаточное оценка включает всю информацию, которая содержится в выборке по исследуемой статистической характеристики генеральной совокупности. Ни одна из рассматриваемых ранее трех оценок не может дать необходимых дополнительных сведений об исследуемом параметр, как достаточное статистическая оценка.

Следовательно, средняя арифметическая выборочная ~ является несмещенной оценкой средней арифметической генеральной х. Фактор несмещенности этой оценки показывает: если с генеральной совокупности взять большое количество случайных выборок, то их средние * <отличались бы от генеральной средней в большую и меньшую сторону одинаково, то есть, свойство несмещенности хорошей оценки также показывает, что среднее значение бесконечно большого числа выборочных средних равно значению генеральной средней.

В симметричных рядах распределения медиана является несмещенной оценкой генеральной средней. А при условии, что численность выборочной совокупности приближается к генеральной (П ~ * N), медиана может быть в таких рядах и состоятельной оценкой генеральной середньои.Що же касается критерия эффективности относительно медианы как оценки средней арифметической генеральной совокупности, можно доказать, что в выборках большого объема среднеквадратичная ошибка медианы (Стме) равен 1,2533 среднеквадратичной ошибки выборочной средней

). То есть Стме *. Поэтому медиана не может быть эффективной оценкой средней арифметической генеральной совокупности, поскольку ее средняя квадратическая ошибка больше средней квадратичной ошибки средней арифметической выборки. К тому же средняя арифметическая удовлетворяет условиям несмещенности и способности, а, следовательно, является лучшей оценкой.

Возможна и такая постановка. Может средняя арифметическая выборки быть несмещенной оценкой медианы в симметричных распределениях совокупности, для которой совпадают значения средней и медианы? И будет выборочная средняя состоятельной оценкой медианы генеральной совокупности? В обоих случаях ответ будет положительным. Для медианы генеральной совокупности (с симметричным распределением) средняя арифметическая выборки является несмещенной и согласованной оценкой.

Помня, что Стме ~ 1,2533ст й, приходим к выводу: средняя арифметическая выборки, а не медиана, более эффективной оценкой медианы исследуемой генеральной совокупности.

Каждая характеристика выборки не обязательно является лучшей оценкой соответствующей характеристики генеральной совокупности. Знание свойств оценок позволяет решать вопрос не только выбора оценок, но и их улучшения. В качестве примера можно рассмотреть случай, когда расчеты показывают, что значения средних квадратичных отклонений нескольких выборок из одной генеральной совокупности во всех случаях оказываются меньше среднего квадратичного отклонения генеральной совокупности, причем величина разницы обусловлена объемом выборки. Умножив значение среднего квадратического отклонения выборки на поправочный коэффициент, получим улучшенную оценку среднего квадратического отклонения генеральной совокупности. За такой поправочный коэффициент используют поправку Бесселя

п а I п

(П - 1), то есть для устранения смещения оценки получают "п - 1 .Такой числовое выражение показывает, что среднее квадратическое отклонение выборки, использовано как оценка, дает заниженное значение параметра генеральной совокупности.

Как известно, статистические характеристики выборочной совокупности является приблизительным оценкам неизвестных параметров генеральной совокупности. Сама оценка может иметь форму одного числа или какой-либо определенной точки. Оценка, которая определяется одним числом, называется точечной. Так, выборочная средняя (~) является несмещенной и наиболее эффективной точечной оценкой генеральной средней (х), а выборочная дисперсия) - смещенной точечной оценкой генеральной

дисперсии () .Если обозначить среднюю ошибку выборочной средней т <> то точечную оценку генеральной средней можно записать в виде х ± т °. Это означает, что ~ - оценка генеральной средней х с ошибкой, равной т ". Понятно, что точечные статистические оценки х и o не должны иметь систематической ошибки в

ooo ~~ o <в 2

сторону завышения или занижения оцениваемых параметров х и. Как было сказано ранее, оценки, которые удовлетворяют такое условие, называются

несмещенными. Что же представляет собой ошибка параметра т "? Это средняя из множества конкретных ошибок:

Точечная оценка параметра генеральной совокупности заключается в том, что с разных возможных выборочных оценок сначала избирается та, которая имеет оптимальные свойства, а затем вычисляется значение этой оценки. Полученное расчетное значение последней рассматривается как наилучшее приближение к неизвестному истинному значению параметра генеральной совокупности. Дополнительные расчеты, связанные с определением возможной ошибки оценки, не всегда обязательные (в зависимости от виришування задач оценки), но, как правило, осуществляются практически всегда.

Рассмотрим примеры определения точечной оценки для средней исследуемых признаков и для их доли в генеральной совокупности.

Пример. Посевы зерновых культур района составляют 20000 га. При 10% -ном выборочном обследовании полей получили такие выборочные характеристики: средняя урожайность - 30 ц с I га, дисперсия урожайности - 4, площадь посевов высокоурожайных культур - 1200 гектаров.

Что знать о величине показателя средней урожайности зерновых культур в районе и которое числовое значение показателя доли (удельного веса) высокоурожайных культур в общей площади зерновых исследуемого

региона? То есть необходимо дать оценку названным параметрам (х, г) в генеральной совокупности. Для расчета оценок имеем:

N = 20000; - = 20000 х 0,1 = 2000; ~ = 30; <т = л / 4; № 2000,

Как известно, избирательная средняя арифметическая является эффективной оценкой

генеральной средней арифметической. Таким образом, можно принять, что

лучшая оценка генерального параметра (^) является 30. Чтобы определить степень

точности оценки необходимо найти среднюю (стандартную) ее ошибку:

иа. п ~ И апреля 2000 ч ППЛ

т = Л - (1--) = - (1--) = 0,04

v п N и2000 2000 ^

Полученная величина ошибки свидетельствует о большой точности оценки. Значение т здесь означает, что при многократном повторении таких выборок ошибка оценки параметра составила бы в среднем 0,04. То есть за точечной

оценке средняя урожайность в хозяйствах района будет х = 30 - 0,04 ц с I га.

Для получения точечной оценки показателя доли посевов высокоурожайных культур зерновых в общей площади зерновых за лучшую оценку может быть принято показатель доли в выборке ¥ = 0,6. Таким образом, можно сказать, что по результатам наблюдений лучшей оценкой искомого показателя структуры будет число 0,6. Уточняя вычисления, следует рассчитать среднюю ошибку этой оценки: т и (1 _ п) и 0.6 (1 - 0.б) (1 = 0,01

v п N v 2000 2000 а

Как видим, средняя ошибка оценки генеральной характеристики равна 0,01.

Полученный результат означает, что если бы многократно повторить выборку с объемом в 2000 га зерновых, средняя ошибка принятой оценки доли (удельного веса) высокоурожайных культур в площади зерновых культур предприятий района была бы ± 0,01. В таком случае Р = 0,6 ± 0,01. В процентном выражении доля высокоурожайных культур в общей площади зерновых района составит в среднем 60 ± I.

Расчеты показывают, что для конкретного случая лучшей оценкой искомого показателя структуры будет число 0,6, а средняя ошибка оценки в той или иной сторону будет примерно равняться 0,01. Как видим, оценка достаточно точна.

Известно несколько способов точечной оценки среднего квадратического отклонения в случаях, когда выборка осуществлена из генеральной совокупности единиц с нормальным распределением и параметр в неизвестен. Простой (наиболее легкой в вычислениях) оценкой является размах вариации (и °) выборки, умноженный на поправочный коэффициент, взятый по стандартным таблицами и который зависит от объема выборки (для малых выборок). Параметр среднего квадратического отклонения в генеральной совокупности можно оценить с помощью вычисленной выборочной дисперсии с учетом числа степеней свободы. Корень квадратный из этой дисперсии дает величину, которая будет использована как оценка генерального среднеквадратичного отклонения).

Используя значение параметра в "вычисляют среднюю ошибку оценки генеральной средней (х ") способом, рассмотренным выше.

Как указывалось ранее, в соответствии с требованием способности уверенность в точности той или иной точечной оценки повышается при увеличении численности выборки. Продемонстрировать это теоретическое положение на примере точечной оценки несколько затруднено. Влияние объема выборки на точность оценки очевиден при исчислении интервальных оценок. О них речь пойдет ниже.

В таблице 39 приведены наиболее часто используемые точечные оценки параметров генеральной совокупности.

Таблица 39

Основные точечные оценки _

Вычисленные различными способами значения оценок могут быть неодинаковы по величине. В этой связи в практических расчетах следует заниматься не последовательным вычислением возможных вариантов, а, опираясь на свойства различных оценок, выбрать одну из них.

При малом количестве единиц наблюдений точечная оценка в значительной мере случайно, следовательно, мало надежная. Поэтому в малых выборках она может сильно отличаться от оцениваемой характеристики генеральной совокупности. Такое положение приводит к грубым ошибкам в выводах, которые распространяются на генеральную совокупность по результатам выборки. По этой причине при выборках малого объема пользуются интервальными оценками.

В отличие от точечной интервальная оценка дает диапазон точек, внутри которого должен находиться параметр генеральной совокупности. Кроме того, в интервальной оценке указывается вероятность, а, следовательно, она имеет важное значение в статистическом анализе.

Интервального называют оценку, которая характеризуется двумя числами - границами интервала, который охватывает (покрывает) оцениваемый параметр. Такая оценка представляет собой некоторый интервал, в котором с заданной вероятностью находится искомый параметр. Центром интервала принимается выборочная точечная оценка.

Таким образом, интервальные оценки является дальнейшим развитием точечного оценивания, когда такая оценка при малом объеме выборки неэффективна.

Задачу интервального оценивания в общем виде можно сформулировать так: по данным выборочного наблюдения необходимо построить числовой интервал, в отношении которого ранее выбранным уровнем вероятности можно утверждать, что в пределах данного интервала находится оцениваемый параметр.

Если взять достаточно большое количество единиц выборки, то, пользуясь теоремой Ляпунова, можно доказать вероятность того, что ошибка выборки не превысит некоторую заданную величину а, то есть

И ~ "*!" А или И № "г. йА.

В частности, эта теорема дает возможность оценивать погрешности приближенных равенств:

- "Р (п и - частота) х" х. п

Если ^ * 2Xз..., х - ~ независимые случайные величины и п, то вероятность их средней (х) находится в пределах от а до 6 и может быть определена уравнениями:

р (а (х (е) 1 е 2 сии,

_а - Е (х); _ в - Е (х) ДЕ ° а

Вероятность Р при этом называют доверительной вероятностью.

Таким образом, доверительной вероятностью (надежностью) оценки генерального параметра по выборочной оценке называют вероятности, с которой осуществляются неравенства:

| ~ Х | <а; | и, ориентир | <д

где а - предельная ошибка оценки, согласно средней и доли.

Границы, в которых с этой заданной вероятностью может находиться генеральная характеристика, называют доверительными интервалами (доверительными границами). А границы этого интервала получили название границ доверия.

Доверительные (или толерантные) границы - это границы, выход за пределы которых данной характеристикой вследствие случайных колебаний имеет незначительную вероятность (Л ^ 0,5; р 2 <0,01; Л <0,001). Понятие "доверительный интервал" введено Дж.Нейман и К.Пирсоном (1950 г.). Это установленный по выборочным данным интервал, который с заданной вероятностью (доверительной вероятностью) охватывает (покрывает) настоящее, но неизвестно для нас значение параметра. Если уровня доверительной вероятности принять значения 0,95, то эта вероятность свидетельствует о том, что при частых приложениях данного способа (метода) вычислений доверительный интервал примерно в 95% случаев будет покрывать параметр. Доверительный интервал генеральной средней и генеральной доли определяется на основе приведенных выше неравенств, из которых

следует, что ~ _А - х - ~ + А; № _А - г. - № + А.

В математической статистике надежность того или иного параметра оценивают по значению трех следующих уровней вероятности (иногда называют "пороги вероятности»): Л = 0,95; ^ 2 = 0,99; Р 3 = 0,999. Вероятности, которыми решено пренебречь, то есть а 1 = 0.05;; а 2 = 0.01; "3 = 0,001 называют уровнями значимости, или уровнями существенности. Из приведенных уровней надежные выводы обеспечивает вероятность Р 3 = 0,999. Каждому уровню доверительной вероятности соответствует определенное значение нормированного отклонения (см. табл. 27). Если нет в распоряжении стандартных таблиц значений интервала вероятностей, то эту вероятность можно вычислить с определенной степенью приближения по формуле:

Р (<) = - = ^ = 1 е "~ й и.

На рисунке 11 заштрихованы те части общей площади, ограниченной нормальной кривой и осью абсцисс, которые соответствуют значению <= ± 1; <= ± 2; <= и 3 и для которых вероятности равны 0,6287, 0,9545; 0,9973. При точечном оценке рассчитывается, как уже известно, средняя ошибка выборки, при интервальном - предельная.

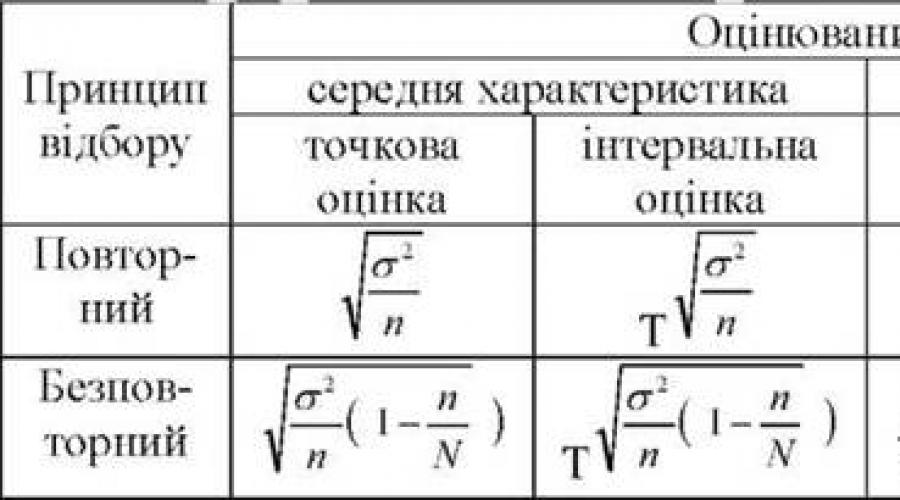
В зависимости от принципов отбора единиц (повторного или без повторного) структурные формулы расчета ошибок выборки

различаются по величине поправки (N).

Рис. 11. Кривая нормального распределения вероятностей

В таблице 40 приведены формулы расчетов ошибок оценок генерального параметра.

Рассмотрим конкретный случай интервальной оценки параметров генеральной совокупности по данным выборочного наблюдения.

Пример. При выборочном обследовании хозяйств района установлено, что среднесуточный надой коров (х) составляет 10 кг. Доля чистопородного скота в общей численности поголовья составляет 80%. Ошибка выборки с доверительной вероятностью Р = 0,954 оказалась равной 0,2 кг; для частного чистопородного скота 1%.

Таким образом, границы, в которых может находиться генеральная средняя

производительность, будут 9,8 <х <10,2; для генеральной доли скота -79 <Р <81.

Вывод: с вероятностью 0,954 можно утверждать, что разница между избирательной средней продуктивностью коров и генеральной производительностью составляет 0,2 кг. Предел среднесуточного надоя - 9,8 и 10,2 кг. Доля (удельный вес) чистопородного скота в предприятиях района находится в пределах от 79 до 81%, ошибка оценки не превышает 1%.

Таблица 40

Расчет точечных и интервальных ошибок выборки

При организации выборки важное значение имеет определение необходимой ее численности (п). Последняя зависит от вариации единиц обследуемой совокупности. Чем больше коливнисть, тем больше должна быть численность выборки. Обратная связь между численностью выборки и ее предельной ошибкой. Стремление получить меньшую ошибку требует увеличения численности выборочной совокупности.

Необходимая численность выборки определяется на основе формул предельной ошибки выборки (д) с заданным уровнем вероятности (Р). Путем математических преобразований получают формулы расчета численности выборки (табл. 41).

Таблица 41

Расчет необходимой численности выборки _

Следует отметить, что все изложенное в отношении статистических оценок основывается на предположении, что выборочная совокупность, параметры которой используются при оценке, полученная с использованием метода (способа) отбора, который обеспечивает получение вероятностей выборки.

При этом, выбирая доверительную вероятность оценки, следует руководствоваться тем принципом, что выбор ее уровня не является математическим задачам, а определяется конкретно решаемой проблемой. В подтверждение сказанному рассмотрим пример.

Пример. Предположим, на двух предприятиях вероятность выпуска готовой (качественной) продукции равна Р = 0,999, то есть вероятность получения брака продукции составит а = 0,001. Можно ли в рамках математических соображений, не интересуясь характером продукции, решить вопрос о том, имела ли большая вероятность нехватки а = 0,001. Допустим, одно предприятие выпускает сеялки, а второе - самолеты для обработки посевов. Если на 1000 сеялок случится одна бракованная, то с этим можно мириться, потому что переплавка 0,1% сеялок дешевле, чем перестройка технологического процесса. Если же на 1000 самолетов встретится один бракованный, это, безусловно, приведет к серьезным последствиям при его эксплуатации. Итак, в первом случае вероятность получения брака а = 0,001 может приниматься, во втором случае - нет. По этой причине выбор доверительной вероятности в расчетах вообще и при исчислении оценок, в частности, следует осуществлять исходя из конкретных условий задачи.

В зависимости от задач исследования может возникнуть необходимость вычисления одной или двух доверительных границ. Если особенности решаемой задачи требуют установки только одной из границ, верхней или нижней, можно убедиться, что вероятность, с которой устанавливается эта граница будет выше, чем при указании обоих границ для одного и того же значения коэффициента доверия 1

Пусть доверительные границы установлены с вероятностью Р = 0,95, то есть,

в 95% случаев генеральная средняя (х) будет не меньше нижнего

доверительного интервала х ™ - х "м и не более верхнего доверительного

интервала Хверх - = х + В этом случае только с вероятностью а = 0,05 (или 5%) средняя генеральная может выйти за указанные границы. Поскольку распределение X симметричный, то половина из этого уровня

вероятности, то есть 2,5% будет приходиться на случай, когда х (х ™ -а вторая половина - на случай когда, х ^ х "^ -. Из этого следует, что вероятность того, что средняя генеральная может быть меньше, чем значение верхней

доверительной границы Хвеи "-, равна 0,975 (то есть 0,95 +0,025). Следовательно, создаются условия, когда при двух доверительных границах мы пренебрегаем

значением х как меньше х "" *., так и большими или Хеерх. Называя

только одну доверительную границу, например, Хверх., мы пренебрегаем только теми ~, превышающих эту границу. Для одного и того же значения коэффициента доверия X уровень значимости а здесь оказывается в два раза меньше.

Если рассчитываются только значение признака, которые превышают

(или наоборот не превышают) значения искомого параметра х, доверительный интервал называется односторонним. Если рассматриваемые значения ограничиваются с обеих сторон, доверительный интервал носит название двустороннего. Из сказанного выше следует, что гипотезы и ряд критериев, в частности критерий Х-Стьюдента, нужно рассматривать как односторонние и двусторонние. Поэтому при двусторонней гипотезе уровень значимости для одного и того же значения X будет в два раза больше, чем односторонняя. Если мы хотим при односторонней гипотезе оставить таким же уровень значимости (и уровень доверительной вероятности), как при двусторонней гипотезе, то величину X следует взять меньше. Эта особенность учтена при составлении стандартных таблиц критериев Х-Стьюдента (приложение 1).

Известно, что с практической стороны чаще представляют интерес не столько доверительные интервалы возможной величины генеральной средней, сколько те максимальные и минимальные величины, больше или меньше которых с заданной (доверительной) вероятностью генеральная средняя быть не может. В математической статистике их называют гарантированным максимумом и гарантированным минимумом средней. Обозначив названные параметры

соответственно через и х ™, можно записать: ХШ ™ = х +; хшип = х ~.

При исчислении гарантированных максимальных и минимальных значений генеральной средней, как границы одностороннего доверительного интервала в приведенных выше формулах, величина 1 берется как критерий односторонний.

Пример. По 20 участках выборки установлена средняя урожайность сахарной свеклы 300 н / га. Данная выборочная средняя характеризует соответствующий

параметр генеральной совокупности (х) с ошибкой 10 н / га. Согласно избирательности оценок генеральная средняя урожайность может быть как больше, так и меньше выборочной средней х = 300. С вероятностью Р = 0,95 можно утверждать, что искомый параметр не будет больше ХШ "= 300 +1,73 х10 = 317,3 ц / га.

Величина 1 взята для числа степеней свободы ^ = 20-1 при односторонней критической области и уровне значимости а = 0,05 (приложение 1). Итак, с вероятностью Р = 0,95 гарантированный максимально возможный уровень генеральной средней урожайности оценивается в 317 н / га, то есть при благоприятных условиях средняя урожайность сахарной свеклы не превышает указанной величины.

В некоторых отраслях знаний (например, в естественных науках) теория оценки уступает теории проверки статистических гипотез. В экономической науке методы статистической оценки играют очень важную роль в деле проверки надежности результатов исследований, а также в разного рода практических расчетах. Прежде всего это касается использования точечной оценки исследуемых статистических совокупностей. Выбор можно лучшей оценки - основная проблема точечной оценки. Возможность такого выбора обусловлена знанием основных свойств (требований) статистических оценок.

является смещенной О. с. для дисперсии , так как ; в качестве несмещенной О. с. для s 2 обычно берут функцию

См. также Несмещенная оценка.

За меру точности несмещенной О. с. а для параметра ачаще всего принимают дисперсию Da.

О. с. с наименьшей дисперсией наз. наилучшей. В приведенном примере среднее арифметическое (1) - наилучшая О. с. Однако если случайных величин X i отлично от нормального, то О. с. (1) может и не быть наилучшей. Напр., если результаты наблюдений Х i распределены равномерно в интервале (b, с ), то наилучшей О. с. для математич. ожидания а= (b+с )/2 будет полусумма крайних значений

(3)

В качестве характеристики для сравнения точности различных О. с. применяют эффективность - дисперсий наилучшей оценки и данной несмещенной оценки. Напр., если результаты наблюдений Х i распределены равномерно, то дисперсии оценок (1) и (3) выражаются формулами

и (4)

Так как оценка (3) наилучшая, то эффективность оценки (1) в данном случае есть

При большом количестве наблюдений побычно требуют, чтобы выбранная О. с. стремилась по вероятности к истинному значению параметра а, т. е. чтобы для всякого e > 0

такие О. с. наз. состоятельными (пример состоятельной О. с,- любая , дисперсия к-рой при стремится к нулю; см. также Состоятельная оценка ). Поскольку важную роль при этом играет стремления к пределу, то асимптотически наилучшими являются асимптотически эффективные О. с., то есть такие О. с., для к-рых при

Напр., если распределены одинаково нормально, то О. с. (2) представляет собой асимптотически эффективную оценку для неизвестного параметра , так как при дисперсия оценки и дисперсия наилучшей оценки асимптотически эквивалентны:

и, кроме того,

Фундаментальное значение для теории О. с. и ее приложений имеет тот факт, что О. с. для параметра аограничено снизу нек-рой величиной (этой величиной Р. Фишер (R. Fischer) предложил характеризовать количество информации относительно неизвестного параметра a, содержащийся в результатах наблюдений). Напр., если независимы и одинаково распределены с плотностью вероятности р(х; а ).и если - О. с. для нек-рой функции g(a).от параметра а, то в широком классе случаев

Функцию b(а) наз. смещением, а величину, обратную правой части неравенства (5), наз. количеством информации (по Фишеру) относительно функции g(a), содержащейся в результате наблюдений. В частности, если а - несмещенная О. с. параметра а, то,

причем количество информации nIa в этом случае пропорционально количеству наблюдений (функцию I(а).наз. количеством информации, содержащейся в одном наблюдении).

Основные условия, при к-рых справедливы неравенства (5) и (6), - гладкость оценки акак функции от X i , а также от параметра амножества тех точек х, где р( х, а )=0. Последнее условие не выполняется, напр., в случае равномерного распределения, и поэтому дисперсия О. с. (3) не удовлетворяет неравенству (6) [согласно (4) эта дисперсия есть порядка n -2 , в то время как по неравенству (6) она не может иметь малости выше, чем п -1 ].

Неравенства (5) и (6) справедливы и для дискретно распределенных случайных величин X i нужно лишь в определении информации I(а). р(х; а ).заменить вероятностью события {Х=х}.

Если дисперсия несмещенной О. с. a* для параметра асовпадает с правой частью неравенства (6), то - наилучшая оценка. Обратное утверждение, вообще говоря, неверно: дисперсия наилучшей О. с. может превышать . Однако если , то дисперсия наилучшей оценки асимптотически эквивалентна правой части (6), т. е. . Таким образом, с помощью количества информации (по Фишеру) можно определить асимптотич. эффективность несмещенной О. с. а, полагая

Особенно плодотворным информационный подход к теории О. с. сказывается тогда, когда плотность (в дискретном случае - ) совместного распределения случайных величин пред-ставима в виде произведения двух функций h(x 1 ,х 2 ,...,х п ).[у( х 1 , х 2 ,..., х n );а], из к-рых первая не зависит от а, а вторая представляет собой плотность распреде-деления нек-рой случайной величины Z=y (X 1 , Х 2 ,.. ., Х п ), наз. достаточной статистикой или исчерпывающей статистикой.

Один из наиболее распространенных методов нахождения точечных О. с.- моментов метод. Согласно этому методу, теоретич. распределению, зависящему от неизвестных параметров, ставят в дискретное выборочное , к-рое определяется результатами наблюдений X i и представляет собой распределение вероятностей воображаемой случайной величины, принимающей значения с одинаковыми вероятностями, равными 1/n (выборочное распределение можно рассматривать как точечную О. с. для теоретич. распределения). В качестве О. с. для моментов теоретич. распределения принимают соответствующие моменты выборочного распределения; напр., для математич. ожидания аи дисперсии s 2 метод моментов дает следующие О. с.: (1) и выборочную дисперсию (2). Неизвестные параметры обычно выражаются (точно или приближенно) в виде функций от нескольких моментов теоретич. распределения. Заменяя в этих функциях теоретич. моменты выборочными, получают искомые О. с. Этот метод, часто приводящий на практике к сравнительно простым вычислениям, дает, как правило, О. с. невысокой асимптотической эффективности (см. выше пример оценки математического ожидания равномерного распределения).

Другой метод нахождения О. с., более совершенный с теоретич. точки зрения,- максимального правдоподобия метод, или наибольшего правдоподобия метод. Согласно этому методу, рассматривают функцию правдоподобия L(а), к-рая представляет собой функцию неизвестного параметра аи получается в результате замены в плотности совместного распределения аргументов x i самими случайными величинами X i ; если X i - независимы и одинаково распределены с плотностью вероятности р(x; а ), то

(если X i распределены дискретно, то в определении функции правдоподобия Lследует плотности заменить вероятностями событий ). В качестве О. с. максимального правдоподобия для неизвестного параметра апринимают такую величину a, для к-рой L(a) достигает наибольшего значения (при этом часто вместо Lрассматривают т. н. логарифмическую функцию правдоподобия ; в силу монотонности логарифма точки максимумов функций L(a).и l(a) совпадают). Примерами О. с. максимального правдоподобия являются оценки по наименьших квадратов методу.

Основное достоинство О. с. максимального правдоподобия заключается в том, что при нек-рых общих условиях эти оценки состоятельны, асимптотически эффективны и распределены приближенно нормально.

Перечисленные свойства означают, что если a есть О. с. максимального правдоподобия, то при

(если Xнезависимы, то ). Таким образом, для функции распределения нормированной О. с. имеет место предельное соотношение

Преимущества О. с. максимального правдоподобия оправдывают вычислительную работу по отысканию максимума функции L(или l). В нек-рых случаях вычислительная работа существенно сокращается благодаря следующим свойствам: во-первых, если a* - такая О. с., для к-рой (6) обращается в равенство, то О. с. максимального правдоподобия единственна и совпадает с a*, во-вторых, если существует Z, то О. с. максимального правдоподобия есть функция Z.

Пусть, напр., независимы и распределены одинаково нормально так, что

поэтому

Координаты а= а 0 и s= s 0 точки максимума функции I( а, s).удовлетворяют системе уравнений

Таким образом, и, значит, в данном случае О. с. (1) и (2) - оценки максимального правдоподобия, причем - наилучшая О. с. параметра а, распределенная нормально (, ), а - асимптотически эффективная О. с. параметра s 2 , распределенная при больших пприближенно нормально (). Обе оценки представляют собой независимые достаточные статистики.

Еще один пример, в к-ром

Эта плотность удовлетворительно описывает распределение одной из координат частиц, достигших плоского экрана и вылетевших из точки, расположенной вне экрана (a - координата проекции источника на экран- предполагается неизвестной). Для указанного распределения математич. ожидание не существует, т. к. соответствующий расходится. Поэтому отыскание О. с. для аметодом моментов невозможно. Формальное применение в качестве О. с. среднего арифметического (1) лишено смысла, т. к. распределено в данном случае с той же плотностью р(х; a), что и каждый единичный результат наблюдений. Для оценки аможно воспользоваться тем обстоятельством, что рассматриваемое распределение симметрично относительно точки х=а и, значит, а - медиана теоретич. распределения. Несколько видоизменяя метод моментов, в качестве О. с. для апринимают т. н. выборочную медиану m, к-рая при является несмещенной О. с. для a, причем если пвелико, то m распределена приближенно нормально с дисперсией

В то же время

поэтому и, значит, согласно (7) асимптотич. эффективность равна . Таким образом, для того чтобы m была столь же точной О. с. для a, как и оценка наибольшего правдоподобия a, нужно количество наблюдений увеличить на 25%. Если затраты на эксперимент велики, то для определения аследует воспользоваться О. с. а, к-рая в данном случае определяется как уравнения

В качестве первого приближения выбирают a 0 =u и далее решают это последовательными приближениями по формуле

См. также Точечная оценка.

Интервальные оценки. Интервальной оценкой наз. такая О. с., к-рая геометрически представима в виде множества точек, принадлежащих пространству параметров. Интервальную О. с. можно рассматривать как точечных О. с. Это множество зависит от результатов наблюдений и, следовательно, оно случайно; поэтому каждой интервальной О. с. ставится в соответствие вероятность, в к-рой эта оценка "накроет" неизвестную параметрич. точку. Такая вероятность, вообще говоря, зависит от неизвестных параметров; поэтому в качестве характеристики достоверности интервальной О. с. принимают доверия - наименьшее возможное значение указанной вероятности. Содержательные стати-стич. выводы позволяют получать лишь те интервальные О. с., коэффициент доверия к-рых близок к единице.

Если оценивается один параметр a, то интервальной О. с. обычно является нек-рый (b, g).(т. н. ), конечные точки к-рого (b и g представляют собой функции от результатов наблюдений; коэффициент доверия со в данном случае определяется как вероятности одновременного осуществления двух событий {b < a} и (g > a}, вычисляемая по всем возможным значениям параметра a:

Если середину такого интервала принять за точечную О. с. для параметра a, то с вероятностью не менее чем со можно утверждать, что этой О. с. не превышает половины длины интервала . Иными словами, если руководствоваться указанным правилом оценки абсолютной погрешности, то ошибочное заключение будет получаться в среднем менее чем в случаев. При фиксированном коэффициенте доверия со наиболее выгодны кратчайшие доверительные интервалы, для к-рых математич. ожидание длины достигает наименьшего значения.

Если распределение случайных величин X i зависит только от одного неизвестного параметра а, то построение доверительного интервала обычно осуществляется с помощью какой-либо точечной О. с. а. Для большинства практически интересных случаев функция распределения разумно выбранной О. с. а монотонно зависит от параметра а. В этих условиях для отыскания интервальной О. с. следует в F(х; а )подставить х= a. и определить корни а 1 = a 1 (a, w) и а 2 =a 2 (a, w) уравнений

(9) где

[для непрерывных распределений ]. Точки с координатами и ограничивают доверительный интервал с коэффициентом доверия w. Разумеется, интервал, построенный столь простым способом, во многих случаях может отличаться от оптимального (кратчайшего). Однако если a - асимптотически эффективная О. с. для a, то при достаточно большом количестве наблюдений такая интервальная О. с. практически несущественно отличается от оптимальной. В частности, это верно для О. с. наибольшего правдоподобия, т. к. она распределена асимптотически нормально (см. (8)). В тех случаях, когда уравнений (9) затруднительно, интервальную О. с. вычисляют приближенно с помощью точечной О. с. максимального правдоподобия и соотношения (8):

где х - корень уравнения

Если , то истинный коэффициент доверия интервальной оценки стремится к w. В более общем случае распределение результатов наблюдений X i - зависит от нескольких параметров а, b,... . В этих условиях указанные выше правила построения доверительных интервалов часто оказываются неприменимыми, т. к. распределение точечной О. с. a, зависит, как правило, не только от a, но и от остальных параметров. Однако в практически интересных случаях О. с. a можно заменить такой функцией от результатов наблюдений X i и неизвестного параметра я, распределение к-рой не зависит (или "почти не зависит") от всех неизвестных параметров. Примером такой функции может служить нормированная О. с. максимального правдоподобия ; если в знаменателе аргументы a, b,... заменить их оценками максимального правдоподобия a, b,. . . , то предельное распределение останется тем же самым, что и в формуле (8). Поэтому приближенные доверительные интервалы для каждого параметра в отдельности можно строить так же, как и в случае одного параметра.

Как уже отмечалось выше, если ,... - независимые и одинаково нормально распределенные случайные величины, то и s 2 - наилучшие О. с. для параметров a и s 2 соответственно. Функция распределения О. с. выражается формулой

и, следовательно, она зависит не только от a, но также и от s. В то же время распределение т. н. отношения Стьюдента

не зависит ни от a, ни от s, причем

где постоянная выбирается так, чтобы выполнялось равенство . Таким образом, доверительному интервалу

соответствует коэффициент доверия

Распределение оценки s 2 зависит лишь от s 2 , причем функция распределения О. с. s 2 аадается формулой

где постоянная D n-1 определяется условием (так наз. -распределением с п-1степенями свободы).

Так как с ростом s вероятность монотонно возрастает, то для построения интервальной О. с. применимо правило (9). Таким образом, если х 1 и x 2 - корни уравнений и = , то доверительному интервалу

соответствует коэффициент доверия w. Отсюда, в частности, следует, что доверительный интервал для относительной ошибки задается неравенствами

Подробные таблицы функций распределения Стьюдента и -распределения имеются в большинстве руководств по математич. статистике.

До сих пор предполагалось, что функция распределения результатов наблюдений известна с точностью до значений нескольких параметров. Однако в приложениях часто встречается случай, когда функции распределения неизвестен. В этой обстановке для оценки параметров могут оказаться полезными т. н. непараметрические методы статистики (т. е. такие методы, к-рые не зависят от исходного распределения вероятностей). Пусть, напр., требуется оценить медиану ттеоретич. непрерывного распределения независимых случайных величин X 1 , Х 2 ,..., Х п (для симметричных распределений совпадает с математич. ожиданием, если, конечно, оно существует). Пусть Y 1 - те же величины X i но расположенные в порядке возрастания. Тогда, если k - целое число, удовлетворяющее неравенствам n/2 , то

Таким образом, - интервальная О. с. для тс коэффициентом доверия w=w n,k . Этот верен при любом непрерывном распределении случайных величин X i .

Выше отмечалось, что выборочное распределение - точечная О. с. для неизвестного теоретич. распределения. Более того, функция Выборочного распределения F n (x).- несмещенная О. с. для функции теоретич. распределения F(x). При этом, как показал А. Н. Колмогоров, распределение статистики

не зависит от неизвестного теоретич. распределения и при стремится к предельному распределению К(у), к-рое наз. распределением Колмогорова. Таким образом, если у - решение уравнения К(y)=w, то с вероятностью w можно утверждать, что функции теоретич. распределения F(у).целиком "покрывается" полосой, заключенной между графиками функций (при различие допредельного и предельного распределений статистики l n практически несущественно). Такую интервальную О. с. наз. доверительной зоной. См. также Интервальная оценка.

Статистические оценки в теории ошибок. Теория ошибок - раздел математич: статистики, посвященный численному определению неизвестных величин по результатам измерений. В силу случайного характера ошибок измерений и, быть может, случайной природы самого изучаемого явления не все такие результаты равноправны: при повторных измерениях нек-рые из них встречаются чаще, другие - реже.

В основе теории ошибок лежит математич. , согласно к-рой до опыта совокупность всех мыслимых результатов измерения трактуется как множество значений нек-рой случайной величины. Поэтому важную роль приобретает О. с. Выводы теории ошибок носят статистич. . Смысл и содержание таких выводов (как, впрочем, и выводов теории О.

Полагая результат измерения Xслучайной величиной, различают три основных типа ошибок измерений: систематические, случайные и грубые (качественные описания таких ошибок даны в ст. Ошибок теория ). При этом ошибкой измерения неизвестной величины аназ. X-а, математич. ожидание этой разности E( Х-а )=b наз. систематической ошибкой (если b=0, то говорят, что измерения лишены систематич. ошибок), а разность d=Х- а-b наз. случайной ошибкой . Таким образом, если приведено пнезависимых измерений величины a, то их результаты можно записать в виде равенств

где аи b- постоянные, a d i - случайные величины. В более общем случае

где b i - не зависящие от d i случайные величины, к-рые равны нулю с вероятностью, весьма близкой к единице (поэтому всякое другое значение маловероятно). Величину b i наз. грубой ошибкой.

Задача оценки (и устранения) систематич. ошибки обычно выходит за рамки математич. статистики. Исключения составляют т. н. метод эталонов, согласно к-рому для оценки bпроизводят серию измерений известной величины а(в этом методе b - оцениваемая величина и а - известная систематич. ошибка), а также , позволяющий оценивать систематич. расхождения между несколькими сериями измерений.

Основная задача теории ошибок - отыскивание О. с. для неизвестной величины аи оценка точности измерений. Если систематич. ошибка устранена (b=0) и наблюдения грубых ошибок не содержат, то согласно (10) Х i =a+d i и, значит, в этом случае задача оценки асводится к отысканию в том или ином смысле оптимальной О. с. для математич. ожидания одинаково распределенных случайных величин X i . Как было показано в предыдущих разделах, вид такой О. с. (точечной или интервальной) существенно зависит от закона распределения случайных ошибок. Если этот закон известен с точностью до нескольких неизвестных параметров, то для оценки, а также для оценки аможно применять, напр., метод максимального правдоподобия; в противном случае следует сначала по результатам наблюдений Х i найти О. с. для неизвестной функции распределения случайных ошибок d i ("непараметрическая" интервальная О. с. такой функции указана выше). В практич. работе часто довольствуются двумя О. с. и (см. (1) и (2)). Если d i распределены одинаково нормально, то эти О. с. наилучшие; в других случаях эти оценки могут оказаться малоэффективными.

Наличие грубых ошибок усложняет задачу оценки параметра а. Обычно доля наблюдений, в к-рых бывает невелика, а математич. ожидание ненулевых |b i | значительно превышает (грубые ошибки возникают в результате случайного просчета, неправильного чтения показаний измерительного прибора и т. п.). Результаты измерений, содержащие грубые ошибки, часто бывают хорошо заметны, т. к. они сильно отличаются от других результатов измерений. В этих условиях наиболее целесообразный способ выявления (и устранения) грубых ошибок - непосредственный анализ измерений, тщательная проверка неизменности условий всех экспериментов, запись результатов "в две руки" и т. д. Статистич. методы выявления грубых ошибок следует применять лишь в сомнительных случаях.

Простейший пример таких методов - статистпч. выявление одного резко выделяющегося наблюдения, когда подозрительным может оказаться либо Y 1 =minX 1 , либо Y п =mахХ i (предполагается, что в равенствах (11) b=0 и закон распределения величин d i известен). Для того чтобы выяснить, обосновано ли предположение о наличии одной грубой ошибки, для пары Y 1 , Y n вычисляют совместную интервальную О. с. (доверительную ), полагая все b i равными нулю. Если эта О. с. "накрывает" точку с координатами (Y 1 , Y n ), то подозрение о наличии грубой ошибки следует считать статистически необоснованным; в противном случае гипотезу о присутствии грубой ошибки надо признать подтвердившейся (при этом обычно забракованное наблюдение отбрасывают, т. к. сколько-нибудь надежно оценить величину грубой ошибки по одному наблюдению статистически не представляется возможным).

Др. Индия . В Ведах и Упанишадах (первых священных книгах Индии XII – VII в.в. до н.э.) наряду с религиозными идеями содержатся умозрительные представления о едином и многосоставном мировом порядке (Рита, Легенда о Пуруши), целостной духовной субстанции (Брахмана), индивидуальной душе (Атмана), перерождении душ (их бессмертии), согласно закону воздаяния (Карма).

Различия между каноническими школами индийской философии (ведантой, санкхъей, йогой, вайшешикой, мимансой) и неканоническими (джайнизмом и буддизмом) заключается в том, что с точки зрения последних интуитивный опыт конкретного человека непосредственно открывает истину и кладется в основу абстрактной системы, а с точки зрения первых – личный опыт приобретает законность, только опираясь на тексты откровений, которые изложены в Ведах.

Религиозно-философские учения того времени получили в основном этическую направленность. Наибольшую известность приобрел буддизм , ставший впоследствии мировой религией. Основная идея буддизма: освобождение от страданий (понимаемое ранним буддизмом как психологическая реальность) путем нирваны (букв. «затухание», «остывание»), когда человек, потеряв все связи с внешним миром, представление о собственном Я, собственные мысли, сливается с неизменной и невыразимой полнотой бытия, как капля впадает в океан.Нирвана – это духовный покой без напряжения и конфликта.

Поскольку главная задача индийской философии заключалась в мокше (спасении), т.е. в высвобождении из круга перерождений (сансары), то древнеиндийские философы чрезвычайно мало внимания уделяли всему внешнему, эмпирическому, преходящему, т. е. природе и обществу. Результатом этого является слабое развитие теоретического естествознания и социологии в Древней Индии. Сосредоточенность на «Я», использование разных психотехник для того, чтобы уйти из этого несовершенного мира, для слияния с первоосновой бытия оставляло большинство философов безразличными к изменениям социального мира и естественного окружения человека.

Оппозицию буддизму составила школа Чарвака. Философы этой школы считали, что единственной реальностью является материя. Все, что есть в мире, состоит из четырех элементов (вода, земля, воздух, огонь). Целью человеческой жизни является наслаждение, а не отказ от желаний.

Др. Китай. Своеобразна культура и философия Древнего Китая. Китайский народ представляет собой загадочное и неповторимое явление в истории: старей­ший из всех существующих, он уже в глубокой древности представлял собой один из образованных и культурных народов. Но, достигнув известной сте­пени цивилизации, и остановились на ней и до настоящего времени сохра­нили ее почти без изменений. Традиционализм как черта китайской цивили­зации сохраняет свою значимость и до наших дней.

Другой китайской особенностью была его географическая изолирован­ность. От всего мира Китай был отгорожен горами, пустынями и морями. Сами китайцы называли свою страну Поднебесная, а себя считали высшей расой и презирали соседние с ними народы.

Китайское государство на всем протяжении его истории – типичная восточная деспотия. Во главе государства – самодержавный правитель с не­ограниченной властью, которая передавалась по наследству. Все китайцы, независимо от своего социального уровня, считались слугами царя.

Жизнь китайцев строго ритуализирована и регламентирована. Различия между слоями общества отражались во всем: образе жизни, одежде и даже в питании. Патриархальный уклад жизни, широко развитый культ предков, религи­озные воззрения оказали влияние на формирование философского мышле­ния.

Следует отметить, что в Др. Китае мифология была слабо развита. Древ­ние китайцы были для этого слишком практичными людьми.

Философия в Китае возникает в период VIII – III в.в. до н.э. Это пе­риод «борющихся царств», в то же время его часто называют «золотым веком китайской философии». В этот период свободно и творчески развивались шесть основных философских школ, среди которых наиболее популярными являлись даосизм и конфуцианство.

В большинстве школ преобладала практическая философия, связанная с проблемами житейской мудрости, нравственности, управления. Кроме того, китайская философия не систематизирована, так как мало была связана даже с той наукой, которая была в Древнем Китае. Она характеризовалась слабым развитием древнекитайской логики, низким уровнем рационализованности.

Осн. школы – конфуцианство и даосизм.

Конфуцианство. Родоначальником древнекитайской философии счи­тается Кун Фу-цзы (Конфуций). Он был историком и государственным дея­телем, основателем учения, которое представляет собой философию морали, облаченную в религиозную форму. Конфуций был причислен го­сударством к лику святых.

Конфуций преклонялся перед древними книгами и вообще перед стари­ной. Большую часть своей жизни он упорядочивал и составлял комментарий к «Книге перемен».

Этическое начало воззрений Конфуция нашло свое выражение его в соот­ветствующих высказываниях и поучениях. Основными принципами эти­ческого учения Конфуция считались следующие:

• взаимность (не делай другому того, чего не желаешь себе («Золотое правило нравственности»);
• человеколюбие (почитание родителей, культ предков);
• сдержанность и осторожность в поступках (осуждение бездеятельно­сти, экстремизма и соглашательства).

Конфуцианцы стремились к осмыслению проблемы места человека в жизни общества и рассматривали возможности становления человека как гражданина, изменения общества в лучшую сторону. Но позитивную мо­дель этих изменений видят не грядущем, а в образцах добропорядочной старины (легенда о золотом веке). Вот почему в конфуцианстве большое значение придается ритуалу, этикету традиции.

На основе своих нравственных принципов Конфуций разработал правила управления государством. Это управление было уподоблено им управле­нию колесницей: справедливый, образованный император правит, чинов­ники – вожжи, закон и мораль – узда, уголовное наказание – вожжи, народ – лошади.

Моделью государственного устройства он считает семью. Отец – госу­дарь, подданные – дети. Конфуций выступал против чрезмерного насилия. «Умело держишь вожжи, лошади побегут сами».

Даосизм . Основоположником традиционно считают Лао-цзы. Даосизм основан на древнем, принадлежащим Востоку миросозерцании, по которому коренной причиной всего существующего признается высшее вечное духовное существо, а человеческие души – излиянием (эманацией) этого существа.

Основные понятия:

ДАО – имеет два значения:

1) субстанция, от которой произошёл весь мир, первоначало, которое представляло собой энергетически ёмкую пустоту. Дао означает всеединое. Оно не имеет ни имени, ни формы; неслышимо, невидимо, непостигаемо, неопределяемо, но совершенно. Оно корень всего, мать всех вещей.

2) путь, по которому должны идти человек и природа, универсальный мировой закон, обеспечивающий существование мира. Лао-цзы ищет пути к гармонии между человеком и Дао. Человек, который способен слиться с Дао (путем) и отказаться от заботы общества, будет счастлив и здоров и проживет долгую жизнь.

ДЭ (добродетель) – проявление Дао. «Незрим образ Дао, когда оно действует, когда оно приносит людям пользу».

У-вэй – отказ от деятельности, вступающей в противоречие с естественными законами природы, и, стало быть, требующей борьбы.

В применении к правителю (а китайские мыслители всегда давали им советы) это звучит так: «Кто служит главе народа посредством Дао, не покоряет другие страны при помощи войск, ибо это может обратиться против него». Война, с точки зрения китайцев – нарушение Дао.

Лао-цзы отверг этические принципы Конфуция, призывая к смирению, состраданию и незнанию. Высшая добродетель, по его мнению, – недеяние и молчание.

Основные идеи философии даосизма :

– всё в мире взаимосвязано, нет ни единой вещи, ни одного явления, которые не были бы взаимосвязаны с другими вещами и явлениями;

– материя, из которой состоит мир, едина; существует кругооборот материи в природе: всё происходит из земли и уходит в землю, т.е. сегодняшний человек вчера был воплощён в виде иных форм, существующих во вселенной, – камня, дерева, частей животных, и после смерти то, из чего состоял человек, станет строительным материалом для иных форм жизни или явлений природы;

– мировой порядок, законы природы, ход истории незыблемы и не зависят от воли человека, следовательно, главный принцип жизни человека – покой и недеяние («у-вэй»);

– особа императора священна, только император имеет духовный контакт с богами и высшими силами; через личность императора на Китай и всё человечество сходит «Дэ», животворящая сила и благодать; чем ближе человек к императору, тем больше «Дэ» перейдёт от императора к нему;

– познать «Дао» и получить «Дэ» можно лишь при полном соблюдении законов даосизма, слиянии с «Дао» – первоначалом, послушании императору и близости к нему;

– путь к счастью, познанию истины – освобождение от желаний и страстей;

– необходимо во всём уступать друг другу.

Лао-цзы отверг этические принципы Конфуция, призывая к смирению и состраданию и незнанию. Высшая добродетель, по его мнению, - недеяние и молчание.

Китайская философия не признает ценности отдельного человека. Она учит индивида не выделяться, не обособляться, подчеркивая мысль о связи всего сущего. Тревожное самочувствие конкретного индивида мало заботит китайского мыслителя. Главное для китайского философа – разумное обуст­ройство космоса, государства. Китайской философии явно недостает челове­ческого содержания. «Она в значительной степени надчеловечна». (П.С. Гуревич.)

Китай – очень древняя страна, имеющая не только богатую культуру, а отличающаяся также своей философией. Следует отметить, что еще Киплинг отмечал, что западу и востоку никогда не сойтись вместе, настолько они разные. Именно древнекитайская философия позволяет наглядно продемонстрировать разницу в культуре и традициях двух сторон света.

Кратко о философии Древнего Китая

Для стран востока китайская философия оказалась таким же катализатором развития мысли и культуры, каковым для остального цивилизованного мира была философия Древней Греции.

Основу философии Древнего Китая составлял принцип триединства Вселенной, которая, по мнению китайских философов, включала в себя небо, землю и человека. При этом вся вселенная состоит из особой энергии, именуемой «Цы», которая в свою очередь подразделяется на женское и мужское начало – инь и янь.

Специфика философии Древнего Китая заключается в том, что на заре своего появления представление действительности и построения миры имело религизно-мифологическую структуру, а все главные действующие лица являлись духами и богами зооморфного характера.

Если говорить об особенностях развития философской школы, то самой значимой в сравнении с остальными философскими течениями, особенностью являлся культ предков, предполагающий приятие факт влияния ушедших в мир иной на судьбу жившего поколения. При этом обязанностями духов была забота о здравствующих.

Вторым отличием является понимание мира как постоянное взаимодействие двух начал – женского и мужского. Согласно верованиям и мышлению, в момент сотворения сущего Вселенная была представлена хаосом, при этом не было разделения на небо и землю. Рождение двух духов – инь и янь, которые стали упорядочивать хаос, привело к разделению Вселенной на два единства, небо и землю. Соответственно ян стал покровителем неба, а инь – покровителем земли. Подобное мировоззрение демонстрирует зачаточность имеющийся натурфилософии.

Также для более полного понимания китайской философии следует иметь в виду, что Китай – это мир культуры правого полушария, что предполагает совершенно иное восприятие действительности. Культуры, которые отличаются развитием правого полушария, концентрируются на зрительных образах, религиозных переживаниях, музыке и гипнозе. Люди подобных культур даже звуки слышат и воспринимают по-другому, поскольку понимание мира у них происходит через конкретные и единичные образы.

Философское мышление Китая включает в себя четыре понятия:

1. Холизм, который выражается в гармоничном единстве человека и мира. Человек и природа не являются противоборствующими субъектами, а представляют собой целостную структуру, стремящуюся к гармонии;
2. Интуитивность. По мнению древнекитайских философов, земная сущность не может быть понята через череду конкретных понятий или найти отражение в семантике языка. Она может быть познана только через интуитивное прозрение;
3. Символизм. В качестве инструментов для мышления древнекитайская философия применяла синсян, что означает образы;
4. Тиянь. Вся полнота принципов макрокосма могла быть постигнута только при помощи серьезного когнитивного акта, который включал в себя познание, эмоциональные переживания и волевые импульсы. Также главенствующая роль в этой схеме уделялось нравственному сознанию.

Философские школы Древнего Китая

Философия Древнего Китая строилась на двух основных учениях, которые имели общие черты, но отличались в деталях мировоззренческих суждений.

Философия Древнего Китая: конфуцианство . Первая из школ, которая является самой известной на сегодняшний день и имеет большое количество последователей. Ее основателем считается Конфуции или Кун Фу-Цзы в китайской транскрипции. Главными постулатами своего учения этот великий мыслитель обозначал благородство, гуманизм и неукоснительное следование правилам поведения и ритуалам. При этом его философия затрагивала управление государством. Конфуции резко негативно относился к насаждению строгих законов, полагая, что люди будут их нарушать априори. Правление следует осуществлять на основе личного примера, что заставит людей понимать и осознать стыд за собственные проступки.

Философия Древнего Китая: даосизм . Еще одно течение, которое также имеет множественных последователей. Его основателем является также реальный человек по имени . Само понятие Дао означает многогранность, которая включает в себя общее единство, бесконечность движения и всемирный Закон. Дао – это всеобщее начало и всеобщий конец. И главное в данном учении, что человек должен всю жизнь стремится к слиянию с Дао, поскольку только это приведет к гармонии, а в ином случае будут несчастья и гибель.